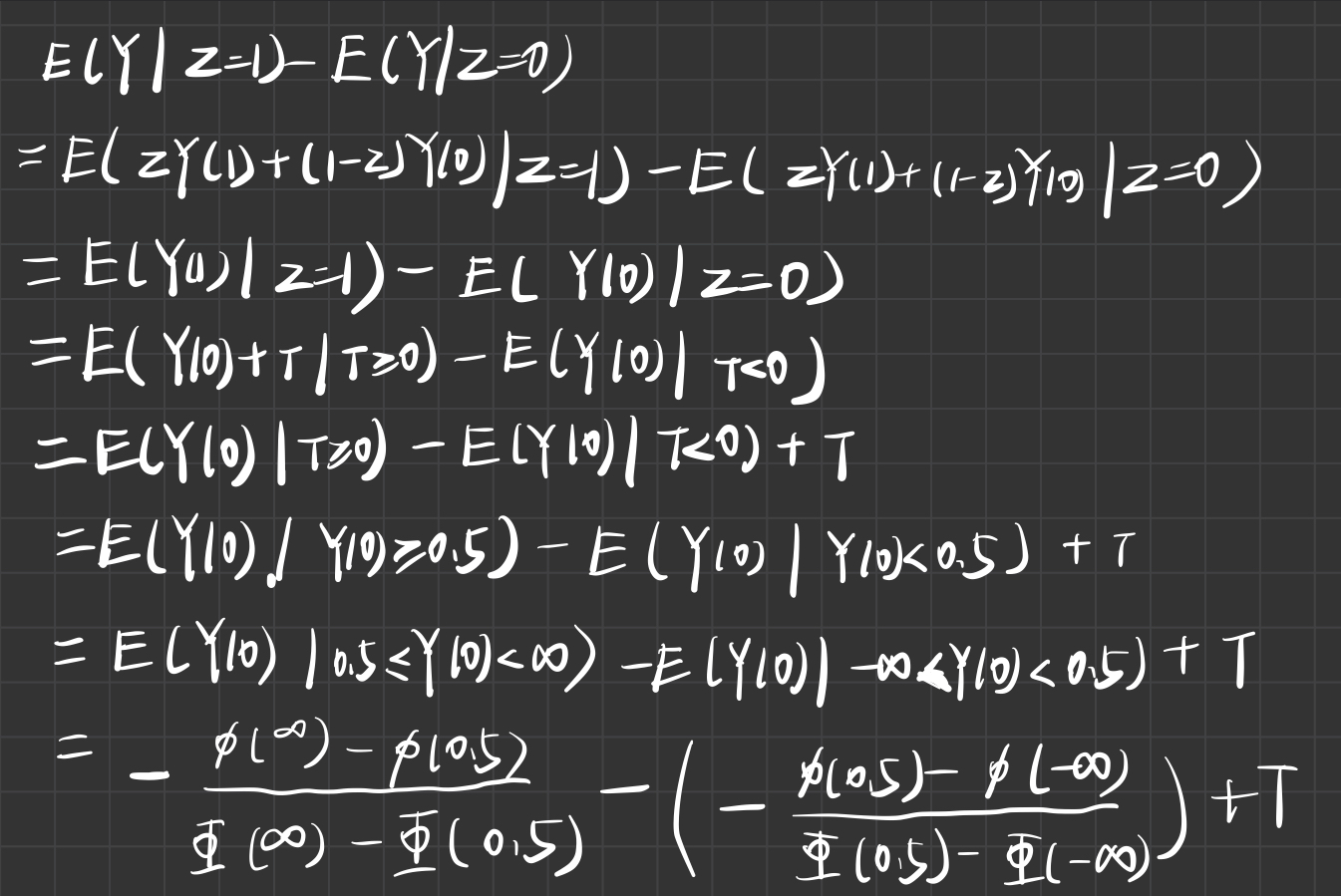causal inference hw 2

高阶

第一章

z <- rbinom(10000,1,0.5)
y <- rbinom(10000,1,0.3)

t <- table(z,y)

rd <- function(x){x[1,1]/(x[1,2]+x[1,1])-x[2,1]/(x[2,2]+x[2,1])}
rr <- function(x){(x[1,1]/(x[1,2]+x[1,1]))/(x[2,1]/(x[2,2]+x[2,1]))}
or <- function(x){(x[1,1]*x[2,2])/(x[2,1]*x[1,2]) }

rd(t)

[1] 0.008762961

rr(t)

[1] 1.012531

or(t)

[1] 1.042926

z <- rbinom(10000,1,0.5)
y <- rbinom(10000,1,z*0.5+0.1)

t <- table(z,y)

rd <- function(x){x[1,1]/(x[1,2]+x[1,1])-x[2,1]/(x[2,2]+x[2,1])}
rr <- function(x){(x[1,1]/(x[1,2]+x[1,1]))/(x[2,1]/(x[2,2]+x[2,1]))}
or <- function(x){(x[1,1]*x[2,2])/(x[2,1]*x[1,2]) }

rd(t)

[1] 0.5078039

rr(t)

[1] 2.296833

or(t)

[1] 13.88793

第二章

-((dnorm(Inf)-dnorm(0.5))/(pnorm(Inf)-pnorm(0.5)))-(-((dnorm(0.5)-dnorm(-Inf))/(pnorm(0.5)-pnorm(-Inf))))+(-0.5)

[1] 1.150238

set.seed(2024)
nsim <- 10 #只是为了多做几次结果看图
outs <- matrix(NA,nsim,3)

for(i in 1:nsim){
  Y1 <- rnorm(10,1,1)
  Y0 <- rnorm(10,-1,1)
  delta1 <- median(Y1)-median(Y0)
  delta2 <- median(Y1-Y0)
  EY <- mean(Y1-Y0)
  out <- c(delta1,delta2,EY )
  outs[i,] <- out
}
outs <- data.frame(delta1=outs[,1],delta2=outs[,2],EY=outs[,3])

plot(density(outs$EY))
lines(density(outs$delta1),col ='red')
lines(density(outs$delta2),col ='blue')

模拟可以看到当Y的样本量较小时，delta2 更贴近平均因果效应 Y的样本量较大时，delta1和dalta2无明显差异（改代码自己跑）

但是MC多次后delta1和delta2 差别不大了

第三章

library(Matching)

Loading required package: MASS

## 
##  Matching (Version 4.10-15, Build Date: 2024-10-14)
##  See https://www.jsekhon.com for additional documentation.
##  Please cite software as:
##   Jasjeet S. Sekhon. 2011. ``Multivariate and Propensity Score Matching
##   Software with Automated Balance Optimization: The Matching package for R.''
##   Journal of Statistical Software, 42(7): 1-52. 
##

data(lalonde)
# z = lalonde$treat
# y = lalonde$re78

model <- lm(re78~.,lalonde)
#model$residuals

tauhat = t.test(model$residuals[z == 1], model$residuals[z == 0], 
                var.equal = TRUE)$p.value
tauhat

[1] 0.2536674

student = t.test(y[z == 1], y[z == 0],
                 var.equal = FALSE)$p.value
student

[1] 0

W = wilcox.test(y[z == 1], y[z == 0])$p.value
W

[1] 0

D = ks.test(y[z == 1], y[z == 0])$p.value

Warning in ks.test.default(y[z == 1], y[z == 0]): p-value will be approximate
in the presence of ties

D

[1] 0

summary(model)

Call:
lm(formula = re78 ~ ., data = lalonde)

Residuals:
   Min     1Q Median     3Q    Max 
 -9612  -4355  -1572   3054  53119 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)   
(Intercept)  2.567e+02  3.522e+03   0.073  0.94193   
age          5.357e+01  4.581e+01   1.170  0.24284   
educ         4.008e+02  2.288e+02   1.751  0.08058 . 
black       -2.037e+03  1.174e+03  -1.736  0.08331 . 
hisp         4.258e+02  1.565e+03   0.272  0.78562   
married     -1.463e+02  8.823e+02  -0.166  0.86835   
nodegr      -1.518e+01  1.006e+03  -0.015  0.98797   
re74         1.234e-01  8.784e-02   1.405  0.16079   
re75         1.974e-02  1.503e-01   0.131  0.89554   
u74          1.380e+03  1.188e+03   1.162  0.24590   
u75         -1.071e+03  1.025e+03  -1.045  0.29651   
treat        1.671e+03  6.411e+02   2.606  0.00948 **
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 6517 on 433 degrees of freedom
Multiple R-squared:  0.05822,   Adjusted R-squared:  0.0343 
F-statistic: 2.433 on 11 and 433 DF,  p-value: 0.005974